This video (realised with Mathematica) shows (a portion of) a properly embedded (smooth) surface in three-dimensional Minkowski space of constant Gaussian curvature. In other words, the induced metric is a hyperbolic metric. The surface (in yellow) is invariant by a parabolic linear 1-parameter group of isometries -- which is what enables us to draw it explicitly, by reducing a difficult non-linear PDE (of Monge-Ampère type) to an ODE problem.
In gray the domain of dependence of the surface, which is the intersection of the cone x^2+y^2<z^2 with the half-plane z>y+1, and is the future of a parabola in Minkowski space. The parabola is in blue. This is a so-called regular domain, and can be interpreted as a deformation of the standard cone x^2+y^2<z^2. The surface itself is asymptotic to this regular domain.
In my paper "Entire surfaces of constant curvature in Minkowski 3-space" (
ArXiv link), joint with Francesco Bonsante and Peter Smillie, we basically prove that
any regular domain contains a unique properly embedded surface of constant Gaussian curvature (hence intrinsically a hyperbolic surface).
But this particular surface has been first studied in my previous paper "Spacelike convex surfaces with prescribed curvature in (2+1)-Minkowski space" (
ArXiv link), joint with Francesco Bonsante. Among other results, we prove that, although being properly embedded, the induced metric on the surface of the video is
not complete. Roughly speaking, this is because the surface approaches the plane z=y+1 (the plane which contains the blue parabola) very quickly, so that there are paths of finite lenght on the surface which escape every compact set.
In fact the surface is intrinsically isometric to (the interior of) a half-plane in the hyperbolic plane H^2, bounded by a geodesic. In a third paper (in preparation) with Francesco Bonsante and Peter Smillie, we prove that a properly embedded hyperbolic surface is always isometric to a subset of the H^2 bounded by geodesics.
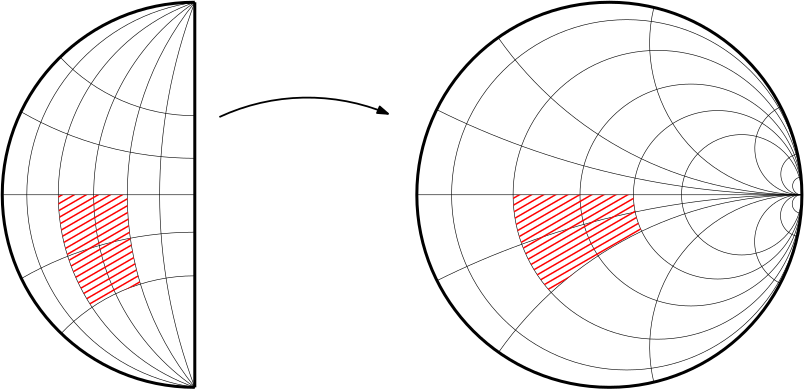
The Gauss map G of the parabolic-invariant surface of the video can therefore be interpreted as a map from a half-plane in H^2 to H^2 itself. In the Poincaré model of H^2, G looks something like the picture below, and has some very interesting properties:
- By general facts, G is minimal Lagrangian, that is, it preserves areas and its graph is a minimal surface;
- G conjugates a 1-parameter hyperbolic group of symmetries to a 1-parameter parabolic group.
One of our goals for future research consists in understanding precisely when this pheonomenon of non-completeness occurs, and how the corresponding minimal Lagrangian maps behave in general. Stay tuned!